MLCV #5 | Image Style Transfer

    3. Computer Vision  Comments

0. Introduction

  • Tasks :
    • Image Style Transfer : The task of migrating a style from one image (Style Image) to another (Content Image).

1. Image Style Transfer using CNNs (2016)

  • Introduction : Introduce a algorithm that can separate and recombine the image content and style of natural images.

  • Method : Extract feature maps $F_l$ from each input image $I_{content} $ and $I_{style}$ using pretrained networks at $l_{th}$ layer. Then, optimize $I_{output}$ to have similar contents with $I_{content}$ and similar style with $I_{style}$.

    1. The content loss between $I_{content}$ and $I_{output}$ is calculated using Frobenius norm at $l_{th}$ layer :

      $$L_{content} = \Sigma(F_{output} - F_{content})^2$$

    2. The style loss between $I_{style}$ and $I_{output}$ at $l_{th}$ layer is calculated using Frob. norm and Gram matrix. The style loss is defined by weighted sum of $L_{style}^l$ :

      $$L_{style} = \sum w_l \cdot L_{style}^l = \sum w_l (\sum(Gram(F_{output}) - Gram(F_{style})))$$

  1. The final obejective function is defined as :

    $$ L_{total} = \alpha L_{content} + \beta L_{style}$$


2. pix2pix (2016)

  • Introduction : Conditional adversarial networks as a general-purpose solution to image-to-image translation problems.
  • Method : The generator translate the input image (gray-scale) to target domain(color). And, the discrimator distinguishes between the converted image and real image.

$$ \text{GAN objective} = arg \min_G \max_D L_{cGAN}(G,D) + \lambda L_{L1}(G) $$

  1. Adversarial Loss , the first term, is from cGAN loss :

    $$ L_{cGAN}(G,D) = \mathbb{E}_y[log(D(x,y))] + \mathbb{E}_x[log(1-D(G(x)))]$$

  2. Reconstruction Loss, the second term, is from traditional CNN based loss, which means pixel-wise differences between $y$ and $G(x)$.

    $$ L_{L1}(G) = \mathbb{E}_{x,y}[| y-G(x) |] $$

  3. Generator architecture is based on U-Net and discriminator architecture is based on PatchGAN(Markovian discrimator).

  4. Generator is fed on real satellite image instead of latent vector and the pair of images are fed into the discriminator.

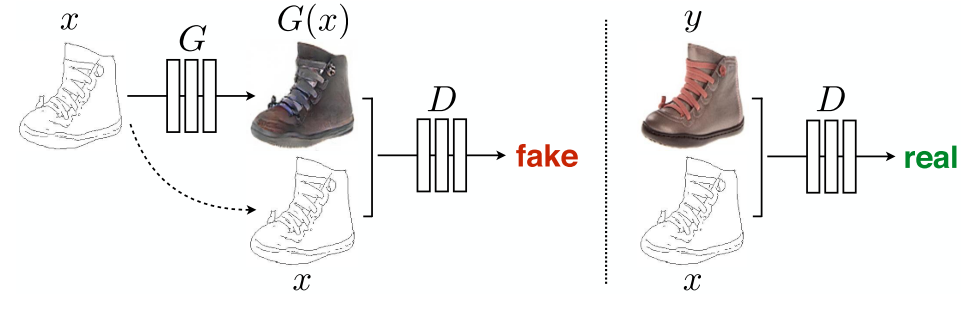
    Figure. Overview of pix2pix Architecture

3. cycleGAN (2017)

  • Introduction : For many tasks, paired training data will not be available. Authors present an approach for learning to translate an image from a source domain $X$ to a target domain $Y$ in the absence of paired examples.

  • Method : using two discriminator (one for discriminating real $y$ and synthesized $G(x)$, the other for real $x$ and synthetic $F(y)$ ). And additional cycle consistency loss for preventing mode collapse that always return same output but very realistic.

$$ L(G,F,D_X,D_Y) = L_{GAN}(G,D_Y,X,Y) + L_{GAN}(F,D_X,Y,X) + \lambda L_{cyc}(G,F) $$

  1. Adversarial Loss : For the mapping function $G: X \rightarrow Y $ and its discrimator $D_Y$, we express the objective as :

    $$ L_{GAN} (G,D_Y,X,Y) = \mathbb{E}{y~p{data}(y)}[(logD_Y(y))] + \mathbb{E}{x~p{data}(x)}[(1-logD_Y(G(x)))] $$

    $$ L_{GAN} (F,D_X,Y,X) = \mathbb{E}{x~p{data}(x)}[(logD_X(x))] + \mathbb{E}{y~p{data}(y)}[(1-logD_X(F(y)))] $$

  2. Cycle Consistency Loss : Adversarial Losses alone cannot guarantee that the learned function can map an individual input $x_i$ to a desired output $y_i$. So authors argue that the learned mapping functions should be cycle-Consistent :

    $$ \text{Forward cycle consistency} = \mathbb{E}{x~p{data}(x)}[| F(G(x))-x |_1 ] $$

    $$ \text{Backward cycle consistency} = \mathbb{E}{y~p{data}(y)}[| G(F(y))-y | _ {1} ] $$

    $$ L_{cyc} (G,F) = \text{forward} + \text{backward} $$

Figure. Overview of cycleGAN Architecture