ML Basic #7 | Sequential Modeling

2019-03-22 2. Machine Learning Comments

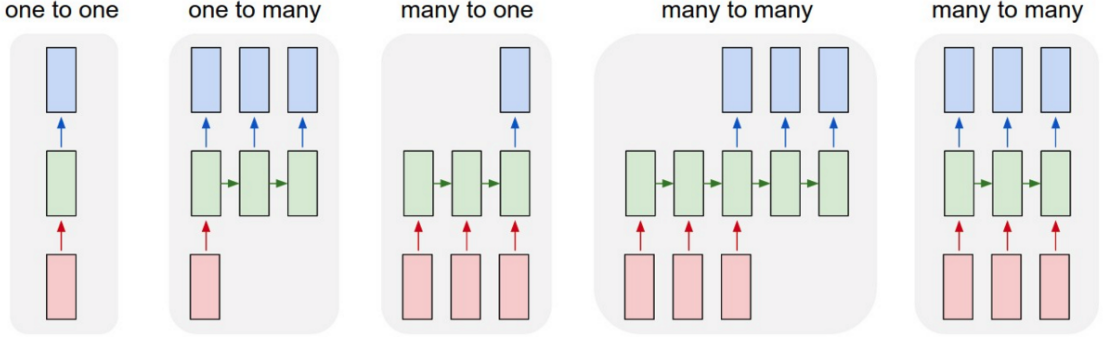
0. Introduction

one to one : Vanilla mode of processing without RNN, from fixed sized input to fixed-sized output
one to many : Sequence output (e.g. image captioning)
many to one : Sequence input (e.g. sentiment analysis)
many to many : Sequence input and sequence output (e.g. Machine Translation)

Figure 1. Overview of Sequence Processing

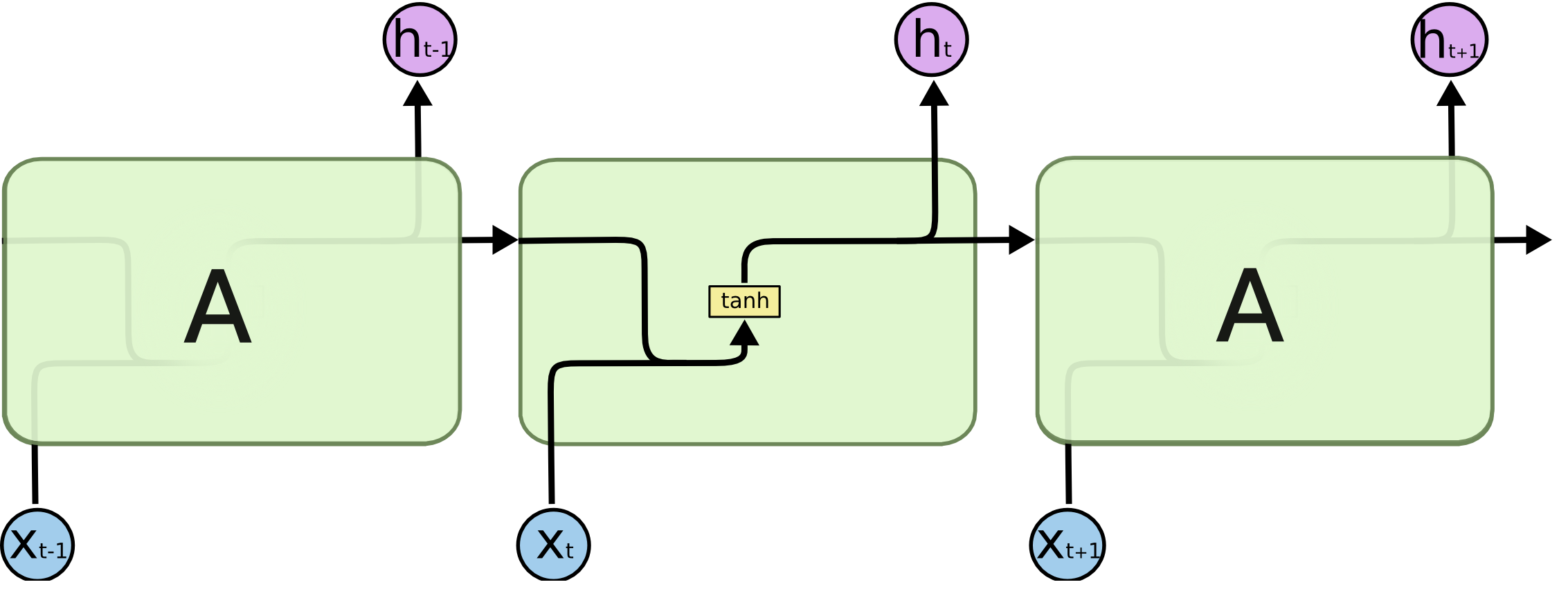
Introduction : Imagine you want to classify what kind of action is happening at every point in a movie. It’s unclear how traditional neural nets could use its reasoning about previous events in the film to predict later ones.
Method : RNN address this issue. They are networks with loops in them, allowing information to persist.
Limitations : Basic RNN design struggles with long-term dependencies (i.e. longer data sequences, paragrph-level rather than sentence-level)

Figure 1. (Above) A standard RNN contains a single layer

Introduction : LSTMs are explicitly designed to deal with long-term dependency problem.
Methods: Internally, LSTMs run with Cell state, which can be thought of as the main stream, with three gates that controlls Cell state (forget gate, input gate, output gate).
1. Forget Gate : The first step in our LSTM is to decide what infromation we’re going to throw away from the cell state. This decision is made by a sigmoid layer called forget gate.
  
  $$ G_f(h_{t-1}, x_t) = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f)$$
2. Input Gate : The next step is to decide what new information we’re going to store in the cell state. This has two parts. First, a sigmoid layer called “input gate” decides which values we’ll update. Next, a tanh layer creates a vector of new candadate values $C_t$, that could be added to the state
  
  $$G_i(h_{t-1},x) = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i)$$
  
  $$\tilde{C} = tanh(W_C \cdot [h_{t-1}, x_t] + b_C)$$
3. Update Cell State: It’s time to update the old cell state, $C_{t-1}$, into the new cell state $C_t$.
  
  $$C_t = f_t * C_{t-1} + i_t * \tilde{C_t} $$
4. Output Gate : Finall, we need to decide what information we’re going to return. This output will be based on our cell state, but will be a filtered version
  
  $$ G_o(h_{t-1}, x) = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o) $$
  
  $$ h_t = G_o * tanh(C_t)$$

Figure 2. An LSTM contains four interacting layers

Figure 3. Step1: decide what information to thow away (L), Step2&3: decide what to store (M), Step4: decide what to output (R)

Introduction : DNNs can only be applied to problems whose inputs and targets can be sensibly encoded with vectors of fixed dimensionality. And this is a significant limitation for sequential problems such as speech recognition and machine translation.
Methods : use one LSTM to read the input sequence, and use another LSTM to extract the output sequence
1. Encoder : tokenized input sentences are fed into encoder that result in context vector
2. Context Vector
3. Decoder : Basically same with RNN Language Model