Linear Algebra for ML #6 | PCA

    1. Linear Algebra  Comments

6.1 Principal Component Analysis

  • Principal component analysis (PCA) : is the process of computing the principal components and using them to perform a change of basis on the data, sometimes using only the first few principal components and ignoring the rest.
  • Principal components : of a collection of n-dim data points are a sequence of $n$ unit vectors, where the $i$-th vector is the direction of a line that best fits the data while being orthogonal to the previous $i-1$ vectors. Here, a best-fitting line is defined as one that minimizes the average squared distance from the points to the line.
  • Methods
    1. 가장 직관적으로 PC를 찾는 방법은 위와 같이 각 데이터로부터 거리가 가장 짧은 축 (벡터) 을 찾고 이를 반복하는 방법
    2. 일반적으로는 주어진 데이터셋의 covariance matrix를 eigendecomposion 하여 얻어낸 eigenvector를 eigenvalue가 큰 순서대로 정렬하여 PC 얻는 방법

C1축으로 투영한 데이터가 분산을 최대로 보존하는것을 알 수 있다.

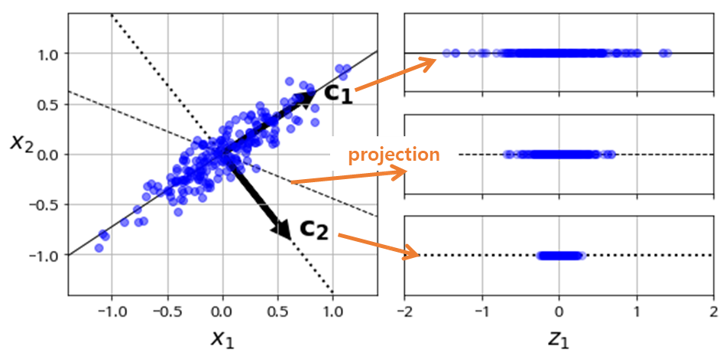
  • PCA는 주어진 n-dim 데이터들을 가장 잘 나타낼수 있는 n개의 벡터 (축) 를 찾는 방법.
  • 이 과정에서 찾아낸 벡터들을 principal component라 부르며 이 principal component (축, 벡터) 위로 데이터를 투영시켜 (projection) 데이터들의 차원을 낮추는데 자주 활용
  • 즉, Principal Components는 주어진 데이터를 가장 잘 나타낼 수 있는 적절한 축 (초평면, 벡터) 이며 이는 곧 원본 데이터의 분산을 최대한 유지 할 수 있는 축이된다. (각 데이터를 구분하는데 필요없는 feature 축을 제거해야 데이터 특성이 유지됨).




2. Covariance Matrix

  • 주어진 데이터셋에서 분산이 최대인 축을 (Principal Components) 찾기위해 앞서 언급했듯 원본 데이터셋과 투영된 데이터셋의 거리가 최소가 되는 축을 찾는 방법도 있겠으나, Covariance Matrix를 선형변환의 하나로 보아 이를 해결하는게 일반적이다.

  • Covariance Matrix : 각 원소 $a_{i,j}$ 가 $i$ 와 $j$ 번째 feature의 covariance로 구성되어 있는 행렬로 x,y 축의 2차원 공분산 행렬의 원소들은 다음의 의미를 갖는다.

    • $a_{11}$ 은 x축 방향으로 퍼진정도, 이 경우 $a_{11}$ 값은 $Cov(X,X) = \sigma_X^2 , \text{ (=variance) }$
    • $a_{22}$ 는 y축 방향으로 퍼진정도, 마찬가지로 값은 $Cov(Y,Y) = \sigma_Y^2$
    • $a_{12} = a_{21}$ 은 x,y축 방향으로 함께 퍼진 정도로 $Cov(X,Y) = E((X-\mu)(Y-v))$

  • Covariance Matrix 를 선형변환으로 보고 아래와 같이 Principal Components 를 얻을 수 있다.

    1. 어떠한 행렬은 선형변환 으로도 볼 수 있으며, 이를 주어진 벡터공간에 곱하여 다른벡터공간으로 mapping 할 수 있다.
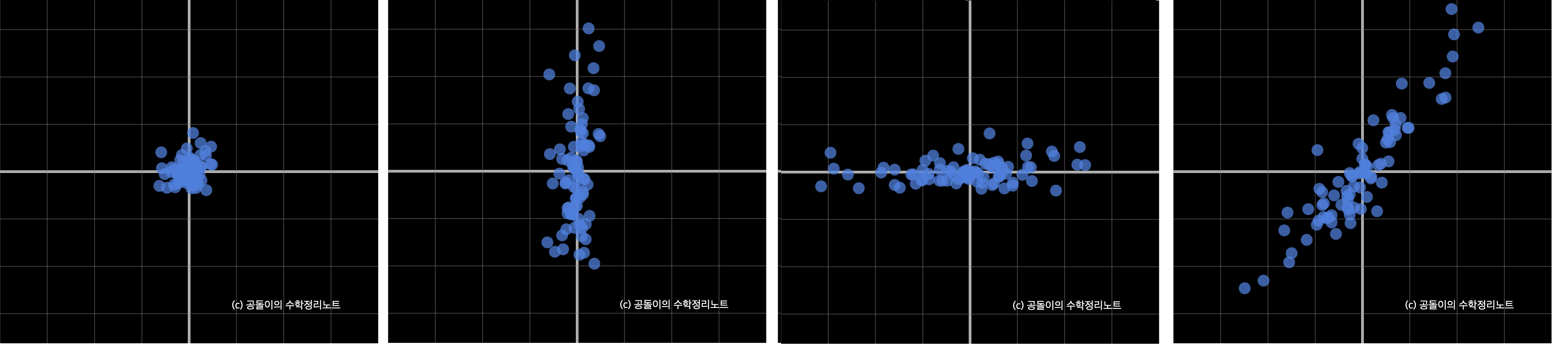
    2. 각 feature들이 선형 독립인, Covariance가 없는 데이터 분포를 가정해보자 (Figure.A below)
    3. 이 데이터 분포에 아래 행렬들을 각각 곱하여 선형변환한 결과는 그림과 같다.
    4. 즉, 선형독립인 데이터분포를 Covariance Mat로 선형변환하면 Covariance Mat의 성분에 따라 X,Y 축으로 Shearing 된 분포를 얻을 수 있다.
    5. 반대로 말하면 우리가 관측을 통해 갖고있는 데이터는 그 데이터의 CovMat에 의해 선형변환된 분포로 볼 수 있으며
    6. 이는 곧, 그 CovMat의 Eigenvector가 선형변환을 통해 방향이 변치 않는 벡터들이고 Eigenvalue가 이 벡터들의 scale된 크기임을 의미한다.
    7. 따라서 우리는 어떤 데이터의 CovMat을 구하고 이 CovMat을 Eigendecomposition하여 Principal Components를 찾을 수 있다
    8. 고유값은 고유벡터의 방향으로 벡터공간이 얼마나 확장될지를 이야기한다. 따라서 Eigendecomposition을 한 이후에 고유값의 크기에 따라 고유벡터를 정렬하면 중요한 순서대로 주성분을 구할 수 있다.

$$ B = \begin{pmatrix} 1 & 0 \\ 0 & 5 \end{pmatrix}. \quad C = \begin{pmatrix} 5 & 0 \\ 0 & 1 \end{pmatrix} , \quad D = \begin{pmatrix} 3 & 2 \\ 2 & 4 \end{pmatrix} $$


(A) original data dist, (B), (C), (D) linearly transformed by matrix B, C, D




3. Implementation

  1. 주어진 데이터의 공분산행렬 Covariance Matrix 를 구하고 이를 eigendecomposition 하여 Eigenvalue와 EigenVector를 구하는방법. 즉 공분산행렬의 고유벡터들이 Principal Component가 되며 이 고유벡터로의 projection (내적) 을 통해 차원축소가 가능하다.

  2. 이미지와 같이 data-dim이 과도하게 커지는 경우 (100x100 이미지의 공분산행렬의 크기는 10000x10000) 공분산행렬을 구하는데 어려움이 있다. 이를 위해 굳이 공분산행렬을 구하지 않고 centerized 데이터를 SVD 하여 Singular Value 와 Singular Vector를 구하는 방법

# (1) Covariance Matrix 의 Eigenvalue 와 Eigenvector를 계산
X_cen = X - X.mean(axis=0)  # 평균을 0으로
X_cov = np.dot(X_cet.T, X_cen) / (N-1)
w, v = np.linalg.eig(X_cov)

# (2) SVD를 이용한 방법
U, D, V_t = np.linalg.svd(x_cen)




4. Applications

  • Dimensionality Reduction : PCA를 통해 PC를 찾고나서 Variance가 큰 순서대로 n개의 basis를 골라 (Eigenvalue가 큰 Eigenvector들) 만든 벡터공간 (hyperplane, 초평면) 위로 데이터를 projection하면 차원축소가 가능하다. 일반적으로 차원을 축소하는 방법은 이러한 Projection을 이용한 방법과 manifold learning 의 두가지 방법론이 있다.

    • 데이터를 표현하는 feature가 증가 → 데이터의 차원이 증가 → 벡터공간에서 부피의 증가 → 데이터의 밀도는 차원이 증가할수록 감소 → 데이터간의 거리 증가 → 고차원, 저밀도의 데이터를 모델링하기 위해 모델이 복잡해짐 → Overfit
    • 예로 어떠한 위치를 표현하기 위하여 X,Y 좌표의 두개 feature를 사용하다가 Z축을 추가하면 2차원에서 3차원이 된다. 그러나 네비게이션과 같이 특정 목적에 따라 굳이 Z축 정보가 필요하지 않을 수도 있다.

    A hyperplane is a subspace whose dimension is one less than that of its ambient space. If a space is 3-dimensional then its hyperplanes are the 2-dimensional planes, while if the space is 2-dimensional, its hyperplanes are the 1-dimensional lines. This notion can be used in any general space in which the concept of the dimension of a subspace is defined.

  • Eigenface: 분산이 큰 순서대로 (Principal Component) 일수록 얼굴의 전반적인 형태를 나타내고, 뒤로갈수록 세부적인 차이를 반영하고 더 뒤로가면 노이즈정보를 나타냄.

  • Noise Reduction : PCA로 얻어진 주성분벡터들은 서로 Orthogonal 이므로 주성분 벡터들이 n차원 공간을 생성하는 basis의 역할도 할 수 있다. 즉 PCA로 얻은 주성분 벡터들을 $e_1, e_2, … e_n$ 이라 하면, 임의의 n차원 데이터 x는 $x = c_1e_1 + c_2e_2 + , … c_ne_n$ 과 같이 나타낼 수 있으며 이와같이 어떤 데이터집합의 데이터들을 그 주성분벡터들의 일차결합으로 표현하는 것을 Karhunen-Loeve Transform 이라한다. 이 때 뒷 부분의 주성분 벡터들은 noise성 정보를 나타내므로 이부분을 제하고 전반부 k개의 벡터들만으로 원래 데이터를 표현하면 노이즈가 제거된 데이터를 얻을 수 있다.

  • Background Subtraction in surveillance camera : 마찬가지로 각 프레임을 데이터 샘플로 보고 PCA를 수행하면 변화가 없는 배경부분이 PC에 해당하므로 이부분을 제거하여 배경제거에도 사용할 수 있다.

  • Whitening : 이상적으로 모든 픽셀이 서로 독립이라면 공분산행렬이 단위행렬이 된다. 즉 위의 그림 (a) 와 같은 형태로 데이터를 변형한다.즉 mean 과 variance를 각각 0과 1로 만드는 작업이라고 볼 수 있을듯.




5. Reference